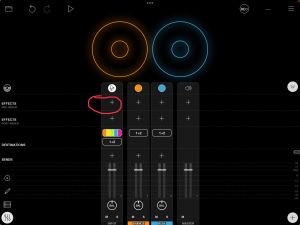
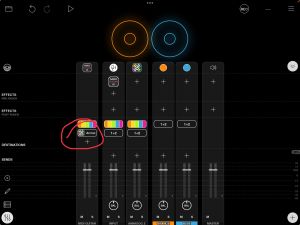
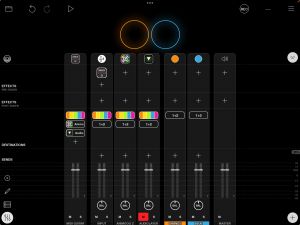
MIDI Guitar 2 works well in Loopy Pro. This page describes how to set it up. For the best results, use the MIDI Guitar AUv3 rather than the IAA version. When setup correctly, you will have MIDI Guitar 2 as an effect on the guitar's input channel and the same instance loaded as a MIDI source in Loopy Pro's mixer as in the picture below.

Setup

Buffer Size Note: MIDI Guitar 2 requires that the buffer size be 256 or smaller. Choose System Settings from Loopy Pro's main menu and make sure the buffer is 256 or smaller

Quick Instructions

In Loopy Pro's mixer:

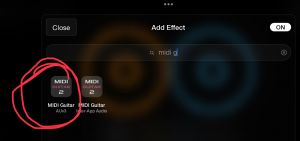
Add the MIDI Guitar 2 AUv3 (not IAA) as a pre-fader effect on the guitar's hardware input channel.
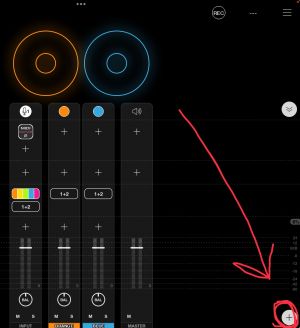
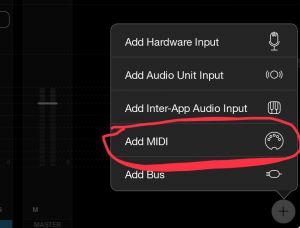
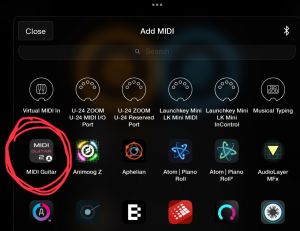
Tap the + sign to add a new mixer channel and choose Add MIDI
Choose the MIDI Guitar 2 instance that appears towards the top of MIDI source popup. It will be marked with an A to indicate that it is an already added instance.
Add any synths that you want to use (preferably AUv3 plugins) to your Loopy Pro mixer
On the MIDI Guitar 2 midi channel, add the synths as destinations.